メカニカル・スペクトロスコピー

メカニカル・スペクトロスコピー

固体に小さな応力を加えたとき，ひずみは応力に比例する，というのがフックの法則ですが，実際の材料の弾性的性質を詳しく調べると，そのような理想的な挙動は示しません．その原因は，材料の中のさまざまな欠陥です．たとえば金属材料中には塑性変形を担う重要な線状欠陥である転位が多数存在します．応力が加えられると転位は応力を緩和するように結晶面に沿って動きますが，その動きによって余分なひずみ（擬弾性ひずみ）が生じます．時間的にやや遅れて現れるこの擬弾性ひずみは弾性エネルギーの損失をひきおこすので，逆にその損失の大きさから欠陥の量を調べることができます． 図1に，さまざまな欠陥を含む金属結晶に周期的応力を加えたときの弾性率と弾性エネルギー損失を模式的に示します．欠陥はそれぞれに動きやすさが異なるので，応力を緩和する速さ，すなわち擬弾性ひずみの現れる速さも欠陥の種類により異なります．周期的応力を加えた場合は振動数と欠陥の動きの速さが同程度のときにエネルギー損失が極大になるという性質があるので，図のように振動数を走査して測定すると，さまざまな欠陥による損失を分離して観測することができます．同時に，弾性率はエネルギー損失の一つ一つの現象に対応して値が変化します．これがメカニカル・スペクトロスコピーです．

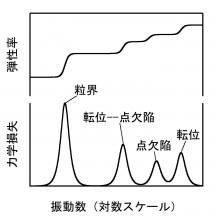図1. 金属多結晶材料の弾性率・力学損失の振動数スペクトル（模式図）.

この手法は1960年頃から鉄鋼材料中の固溶炭素・窒素の定量に利用され，また1970-80年代には原子炉材料として有望視された高融点遷移金属の格子欠陥の基礎研究において重要な役割を果たしました．私たちのグループでは，この手法を用いていろいろな新材料の格子欠陥・拡散・相変態の研究を行っています. もう少し詳しく知りたい方は，沼倉による解説などを読んでみてください．