気液二相流の直接数値計算

  • 気液二相流の直接数値計算法の開発

気体と液体の二相から形成されるいわゆる気液二相流では，両者の密度の相違，界面における表面張力による圧力ジャンプや界面のトポロジー変化等のために，流れ場を精度良く解析することは難しいとされている．本テーマでは，界面を挟んで不連続な物理量を適切に評価しながら界面を捕獲する解析手法(Level Set法やGhost Fluid法など)を導入して，複雑な気液二相流の場を解析するための3次元直接数値解法の開発を行う．

    • Level Set法によるシミュレーション

Level Set法では，界面の位置を捕獲するためには，Level Set関数φを用いる．Level Set関数φは，界面から測った符号付きの距離関数であり，φ=0の集合が界面を表し，φ>0の領域が一方の流体を，φ<0の領域がもう一方の流体を表す．Level Set関数は，以下のLevel Set方程式により，時間発展される．

　　　　　　　　∂φ/∂t+u·∇φ=0

ここで，tは時間，uは流体の速度ベクトルでありる．Level Set関数は時間発展すると，流れにより歪められるため，正しい距離関数ではなくなる．これを是正するために，Level Set関数の再初期化が必要となる．Level Set関数には，質量が保存されないという問題があるため，様々な改善法が提案されている．以下の図は，質量の保存性を改善した三次元Level Set法を用いて，気泡の水面への衝突に伴う水柱の形成をシミュレートした結果である．水柱の形成後の液滴の形成も捕えられている．

 

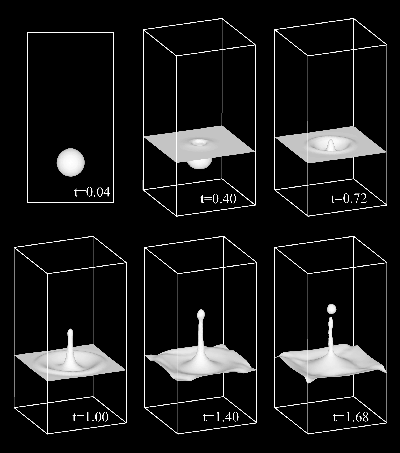
             bubble_burst                       
                                                                  Fig. 1   Bubble bursting at a free surafce           

    1. H. Takahira, T. Horiuchi, S. Banerjee, “An improved three-dimensional level set method for gas-liquid two-phase flows,” ASME Journal of Fluids Engineering, 126, 578-585, (2004). 

                                           

    • Ghost Fluid法による数値シミュレーション

Ghost Fluid法では，界面での境界条件を陽的に当てはめる代わりにGhost Fluidと呼ばれる仮想流体を定義して二相問題を二つの単相問題に帰着させ，陰的に界面での境界条件を満足させる．界面は，Level Set関数で捕獲するものとする．

             GFM
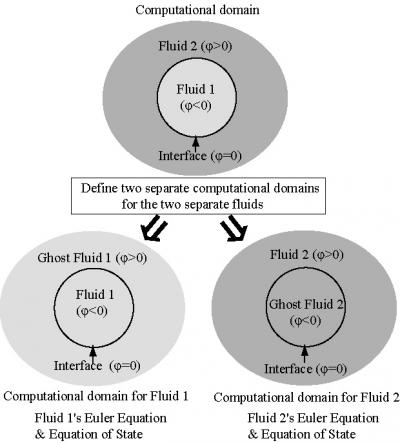
                                                                              Fig. 2 Ghost fluid method

上図のように，φ<0の領域に流体1，φ>0の領域に流体2が存在するものとすると，φ<0の領域にφ>0の領域に実在する流体2の仮想的な流体(Ghost Fluid 2)を定義する．同様に，φ>0の領域にφ<0の領域に実在する流体1の仮想的な流体(Ghost Fluid 1)を定義する．これにより，流体1とGhost Fluid 1を合わせて一つの流体が計算領域全体に定義され，同様に，流体2とGhost Fluid 2を合わせてもう一つの流体が計算領域全体に定義されたことになる．全計算領域で二種類の流体が定義されたことにより，それぞれの流体について独立に単相流の問題として支配方程式を解くことができ，各格子点で次の時間ステップでの二種類の物理量を求めることができる．次に，Level Set方程式を次の時間ステップでの界面位置を求めるために解く．そして，次の時間ステップでのLevel Set関数の符号に基づき，φ<0の領域では流体1の物理量を採用して流体2の物理量を捨てる．同様に，φ>0の領域では流体2の物理量を採用し流体1の物理量を捨てる．これにより，次の時間ステップでの物理量が各格子点でただ一つに決定される．この手順を繰り返して任意の時間での各物理量を求める．

Ghost Fluid法には，流体の圧縮性や界面のトポロジー変化を容易に扱える利点があり，仮想流体の持つ値を，境界条件を満足するように適切に定義することにより，非平衡相変化に伴う温度ジャンプや圧力ジャンプを扱えるため，本研究室では非平衡相変化を考慮した気泡崩壊の解析を行ってきた．Euler的な解析手法は，界面形状が格子解像度に大きく依存する問題があるため，気泡崩壊のような気泡体積が非常に小さくなる際の界面を精度良く捕えるには，Adaptive Zonal Gridsの導入など工夫も必要である．以下の図は，流路中央で生成した単一のレーザ誘起気泡の崩壊をGhost Fluid法でシミュレートした結果の一例である．気泡はその収縮時に，流路中央で二つに分離し，分離した各気泡は，上下の流路壁面に向って並進移動し，それぞれ，上下壁面に向って液体ジェットを形成し，ジェットが界面を貫通する際に衝撃波が発生する．この衝撃波が壁面損傷の要因となる．

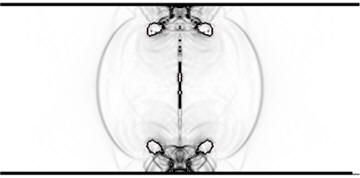
             bubble_collapse      
　　　                                                      Fig. 3 Bubble collapse in a narrow channel

      1. Y. Jinbo, T. Ogasawara, H. Takahira, “Influence of the nonequilibrium phase transition on the collapse of inertia nonspherical bubbles in a compressible liquid,” Experimental Thermal and Fluid Science, 60, 374-384, (2015).
      2. 小林一道, 神保佳典, 高比良裕之, 液体中での衝撃波と気泡との干渉問題へのマルチグリッドGhost Fluid 法の適用, 日本機械学会論文集B編, 77, 20-32 (2011).