なぜ冷やすのか？（つづき）

量子力学か否か？

ある系を考えるときに，その系を記述するのに量子力学を適用するべきか，古典力学・流体力学を用いるべきか，悩むことがある．多粒子系において，量子力学が決定的な影響を及ぼすのは，構成要素である１粒子の波動関数が重なり合うかどうか？という点で見るのがわかりやすい．初等的な量子力学では，粒子にはド・ブロイ波長なる固有の長さスケールが存在する．量子統計力学には，古典統計（マクスウェル統計）を使うべきか，量子統計（フェルミ統計・ボース統計）のどちらを使うべきか？という判断を下すのに便利な指標がある．すなわち，単純な粒子数密度 N/Vと位相空間の体積から求めた密度である次の式(2)の n を比較し，

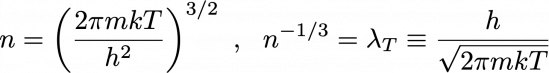  (2)

N/V << n の場合は古典統計でよいが，N/V >> n の場合は量子統計を使え，ということになる．h はプランク定数である．ここで，n の３乗根をとったものを熱的ド・ブロイ波長λ_Tと呼ぶ．温度が下がって λ_Tが平均粒子間隔 (V/N)^1/3 より長くなると，粒子の波動関数の広がりが互いに重なり合うようになることがわかる．そして，絶対零度において無限にながい波長を持つから，絶対零度においては１粒子が節のない定常波のような状態になっていることが予言される．これが多粒子系であるのだから，すべての波動関数が干渉しあって異常な状態になっていることが予想される．それがどんな状態であるか調べるのが，低温物理学である．

また，熱的ド・ブロイ波長λ_Tは軽い粒子ほど低温で伸びやすいこともわかる．重たい粒子よりも軽い粒子の方が，より高温で量子現象が起こるから，実験としては好都合である．そして，実験的に扱いやすい軽い粒子といえば，電子，水素原子，水素分子，³He原子，³He原子であろう．これらはすべて，低温物理学が扱う粒子になりうる．