なぜ冷やすのか?
温度とは何か?
熱力学の第0法則
物体 A と物体 B が熱平衡にあるとき,同時に物体 B と物体 C が熱平衡にあるならば,物体A と物体 C も熱平衡にある.
「そんなの当たり前だろう?」という点を律儀に定義した法則である.
そもそも平衡とは「物体 A と物体B が平衡になっているのであれば,AとBの関係を記述するパラメータがそれ以上待っても変化しない」ということを意味する.熱力学は,粒子の移動のない純粋な熱的な現象の平衡において,熱さ冷たさを表す唯一のパラメータが「温度」であると規定する.ということは,熱力学の第0法則は「A・B・Cなる3つの物体が互いに熱平衡状態にあって,物体 A と物体 B の温度が等しいのであれば物体 B と物体 C の温度も等しい」ということを意味している.「温度計を使って温度を測る」ことの論理的正当性を担保していることにもなる.
この法則が持つ意味を納得できない人は,次の問いに向き合って欲しい:
物体Aとして金属片,物体Bとして木片を冷たい場所で長時間接触させ,温度計により両者の温度が同一になったことを確認したあと,両者を手(物体C)で触ってみると木片よりも金属片のほうが冷たく感じられる.これをもって「金属片と木片が熱平衡になっていなかった証拠である」とする主張に反論できますか?
熱量の希釈と絶対零度
高温TA0である物体 A と低温TB0物体 B を接触させて熱平衡に向かうとき,熱平衡温度T0になるまでの間に物体 A から物体 B に移動した量を熱量と呼ぶ.温度と熱量は熱力学の第 0 法則によって同時に導かれる量で,片方だけでは意味をなさない.
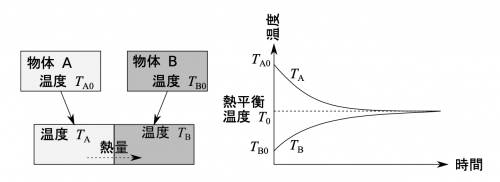
また,熱的接触を繰り返すような熱力学過程だけを用いるなら,熱平衡状態としての絶対零度には決して到達できないという制約があることもわかる.物体 A の温度を下げるためには,A よりもさらに低い温度の物体 B を用意しなければならない.これは別の言い方をすれば,単純な熱的接触だけでは仮に絶対零度の物体を用意したとしても,絶対零度には到達できないともいえる.これは砂糖水を真水で希釈し続けても絶対に真水に到達できないのと同義である.したがって,誰も到達したことのない低温に到達するため,あるいは絶対零度に挑戦するためには単なる熱接触方冷却を用いるだけではダメである.実際には,多くの場合粒子の移動を伴う蒸発冷却を用いる.
冷やすと何が起きるか?
気体分子運動論的アプローチ
気体分子運動論によれば気体分子の運動エネルギーはすべて熱エネルギーに起因し,温度 T [K] 質量 m [kg] の分子の平均的な速度は,
![]() (1)
(1)
で記述される.ここで,k はボルツマン定数である.式(1)から,温度とは分子の運動エネルギーを表す量であることもわる.温度が低いと言うことは分子の運動が抑制されていることになるのだが,絶対零度で粒子の運動は止まってしまうのだろうか? 答えは「状況による」である.すなわち,相互作用のない理想気体の古典的気体分子運動論を展開する限り,絶対零度で粒子の運動は止まってしまう(実際には単に固化してしまう)が,相互作用と量子力学的効果を考慮すると別の何かが起こる可能性がある.
熱力学の第3法則と統計力学的エントロピーによるアプローチ
熱力学の第3法則は,「化学的に均一なすべての固体または液体のエントロピーは絶対零度ではすべて0になる」ことを予言する.ただし,純粋な熱力学においてエントロピーは便宜的な量でありほとんど物理的な意味を持たない.そこで,ボルツマンの原理「孤立した系のエントロピー S は,与えられた条件のもとで系がとりうる微視的状態の数 W の対数に比例し,S=k log W と表わされる」と合わせて考えよう.そうすると,「冷やすと系がとりうる微視的状態の数は減り,絶対零度においては1通りのみになる」ということになる.また,クラジウスの定式化によれば温度とエントロピーの間には dQ = T dS の関係があるから,熱量 Q を奪いながら冷却するということは,エントロピー(状態の数)を減らすという意味になる.すなわち,温度によって乱され隠されていた系の本質が,低温にすることによって顕になる可能性がある.
理想気体の古典的気体分子運動論においては「絶対零度で気体分子は静止する」というが,実際には静止どころではなく「全粒子が整然と並んで静止する」ということになる.これは完全結晶を想像させる.では,量子力学の効果が大きいような系は絶対零度においてどう振る舞うのだろうか?