研究テーマ

複雑系の数理モデリング

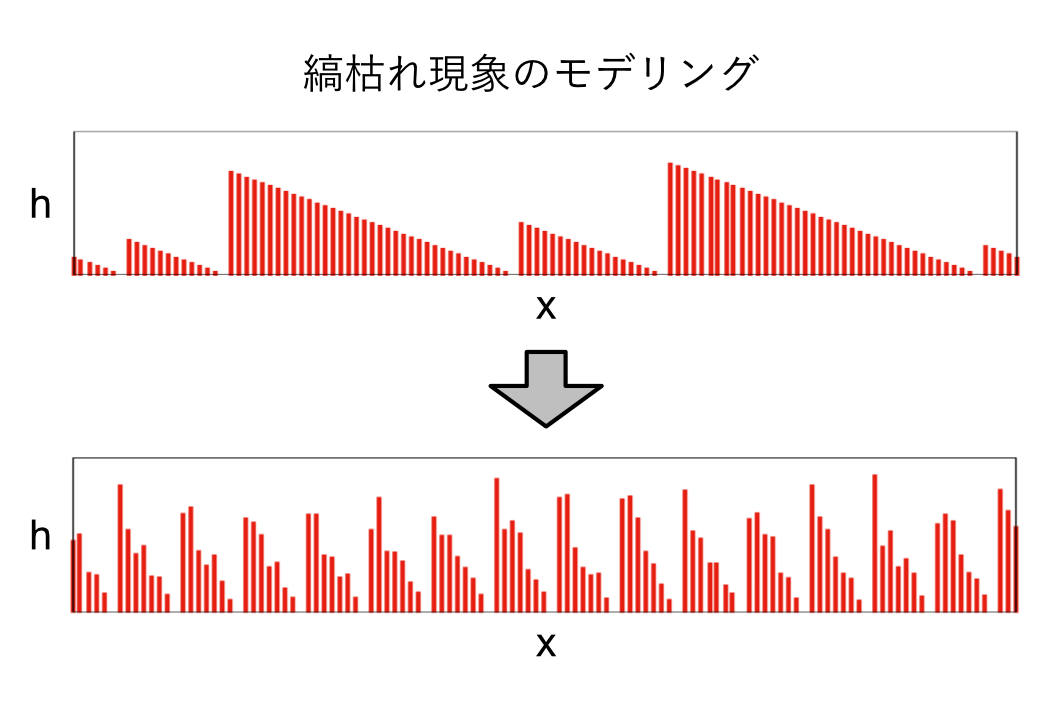
生物群集や人間社会など、相互作用しつつ自律的に運動する無数の個体からなる系を複雑系と言います。 こうした系は全体として、単独の個体が持たない新たな性質を獲得することがあります。 例えば魚の群れや昆虫のコロニーなどに注目すると、各々の個体は勝手気ままに行動しているだけですが、群れ全体としては驚くほど複雑で知的な振る舞いを見せることがあります。 本研究では、このような複雑系のダイナミクスをモデル化し、それを解析することで、現象の背後にある普遍的な数理構造を明らかにすることを目指しています。 （下図：強風によって山肌の樹木が縞状に枯れる「縞枯れ現象」のシミュレーション。個々の棒グラフは木を表している。）

ソフトマターの非平衡ダイナミクス

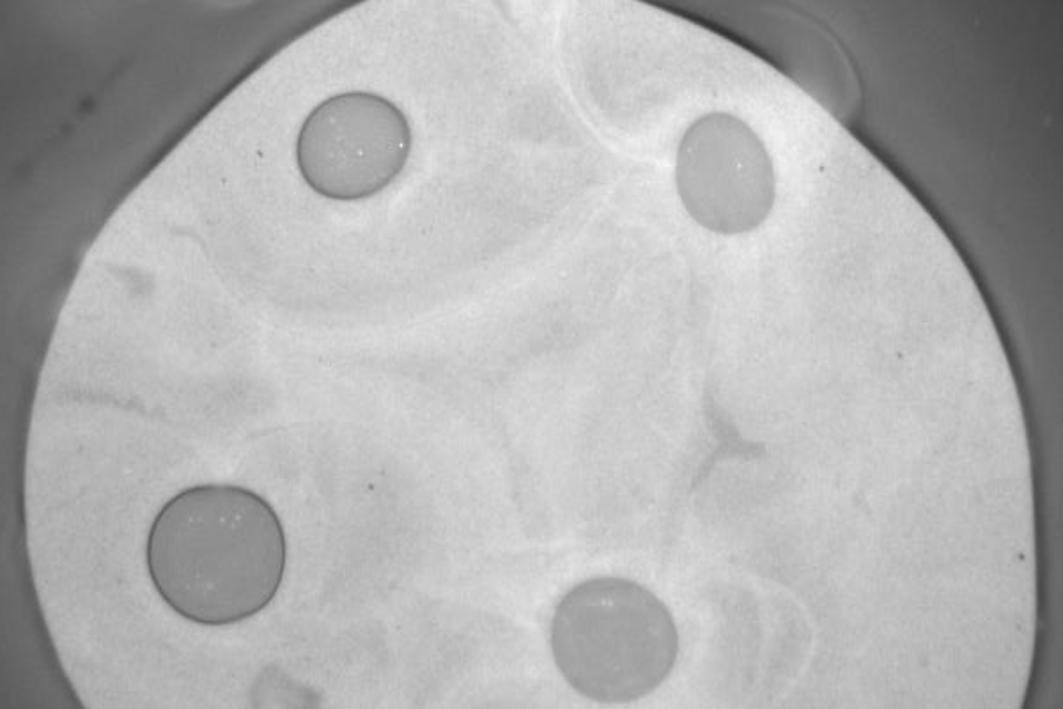
棒状分子や両親媒性分子のように形状や電荷密度に偏りをもつ分子が多数集まると、ミセルや膜といった階層性のある構造を生じ、大きな内部自由度をもつようになります。 ソフトマターなどの言葉で総称されるこのような系は、弱い外場に対しても系の状態が平衡から大きく外れ、大きな応答(非線形の応答)を示すことが特徴です。 本研究では、ソフトマターの相転移・相分離・溶解現象、および外場や欠陥などによる運動を実験や現象論的モデルから研究しています。 （下図：相分離したイオン液体。穴のような構造が自発的に生まれたり、消えたりを繰り返す。）

古典・量子カオス力学系の普遍的振る舞い

古典力学や量子力学の講義でよく扱われる調和振動子や水素原子などは、厳密に解くことが可能な特殊な系です。 こうした系に新たな自由度を一つでも加えると、多くの場合解析的な解は存在しなくなり、系は複雑で予測不可能な振る舞いを示すようになります。 この現象は「カオス」として知られています。 カオスは、決定論的な力学法則に支配されるミクロの世界から、不確かで揺らぐマクロの世界がどのようにして生まれるのかを理解するカギとなる概念です。 本研究では、古典系や量子系に見られる様々なカオス的振る舞いに潜む統一原理を、シンプルな「おもちゃモデル」の解析を通して明らかにすることを目指します。

量子多体系の非平衡ダイナミクス

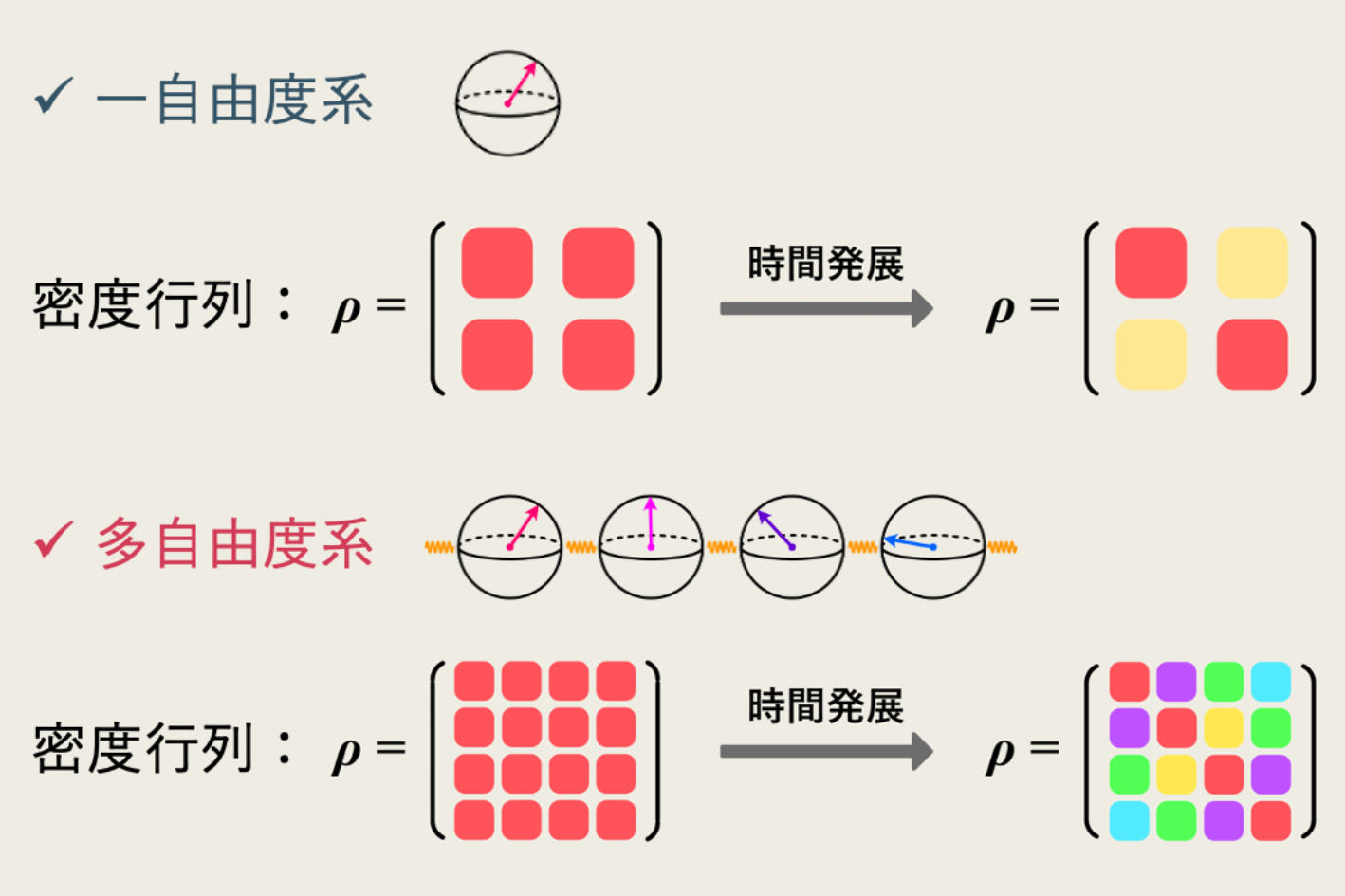
「量子多体系」とは、文字通り多くの粒子からなる量子系のことです。 金属や磁性体なども無数の電子や原子核からなる量子多体系です。 こうした系は長い時間放置すると熱的な平衡状態に落ち着きます。 熱平衡状態にある量子多体系の性質は統計力学によって計算することができ、長年にわたってよく調べられてきました。 さてそれでは、この系を外から強い場を加えることで「揺さぶった」ときに何が起こるでしょうか？ 金属などの固体では、こうした強い非平衡状態を作ることは困難ですが、真空中で原子集団を自在に制御する量子シミュレーションの技術を使えば、人工的にこのような状態を実現することは可能です。 注意すべき点は、この系はもはや熱平衡状態にはないので、統計力学の理論は使えないことです。 本研究テーマは、こうした非平衡状態に駆動された量子多体系のダイナミクスを理論計算とコンピューターを使って明らかにすることです。

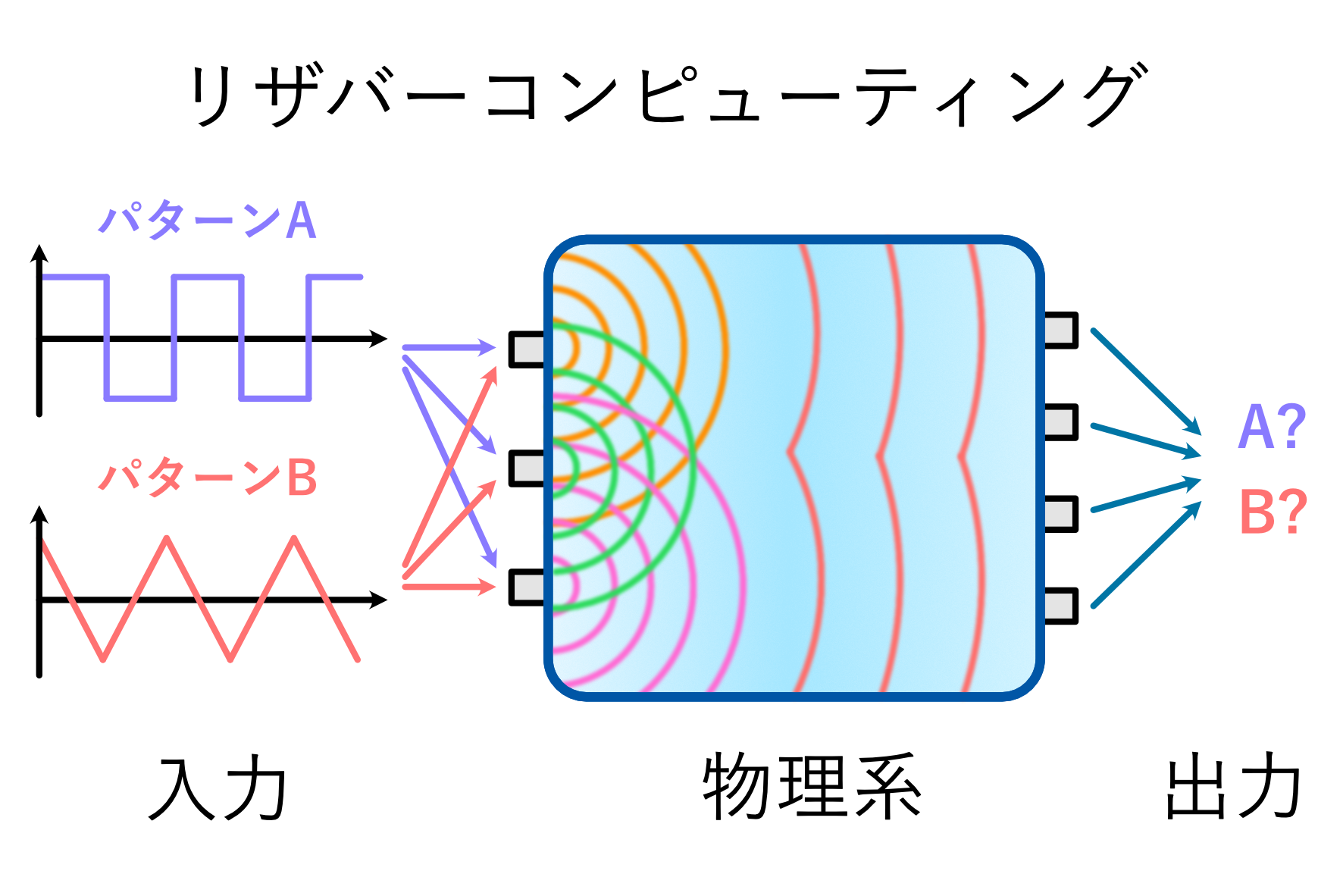
物理系のダイナミクスを用いた機械学習の実現

機械学習は、大量のデータを使って予測や分類をする技術のことを指します。例として、多数の画像から特定の物を見分ける能力や、過去のデータを基に未来の動きを予測する能力があります。これまで、この技術は主にソフトウェアで実現されてきましたが、最近では物理的に機械学習を実現する研究が注目されています。その結果、さらに高速で省エネな学習や予測が期待されています。本研究では、効率的な学習に最適な物理系の性質を非線形力学の手法を用いて明らかにし、それを基に実用的な物理機械学習のデザインを提案することを目指します。（下図：物理機械学習の一種である、リザバーコンピューティングの模式図。入力信号に対する物理系の応答を観測することで、入力信号を分類することができる。）