Ultracold Fermions (Li)

量子シミュレーション：冷却原子実験で初期宇宙・中性子星・未来への旅

フェルミ粒子であるリチウム６原子と、ボース粒子であるリチウム７原子を100nK程度まで冷却し、レーザー光、磁場、ラジオ波を用いてそれらの内部状態や外部状態を自由に制御し、量子シミュレーション実験という新しい手法で、クォークから原子核、中性子星、星間分子等の量子系の基礎研究を進めています。
冷却原子系は自由な発想と巧みな制御により無限の可能性を秘めています。量子系をありとあらゆる切り口から研究することにより、未来の革新技術の１つになり得る量子科学技術が生まれる可能性が大いにあります
物理が大好きな方、量子系に興味のある方、未来を創造したい方、大歓迎です！！
intro

現在参画中の研究プロジェクト

新学術領域研究「量子クラスターで読み解く物質の階層構造」総括班
計画研究「物質の階層変化および状態変化に伴う普遍的物理」代表
研究分担者：大橋洋士（慶應義塾大学）、飯田圭（高知大学）
研究期間 (年度)：2018-06-29 ~ 2023-03-31
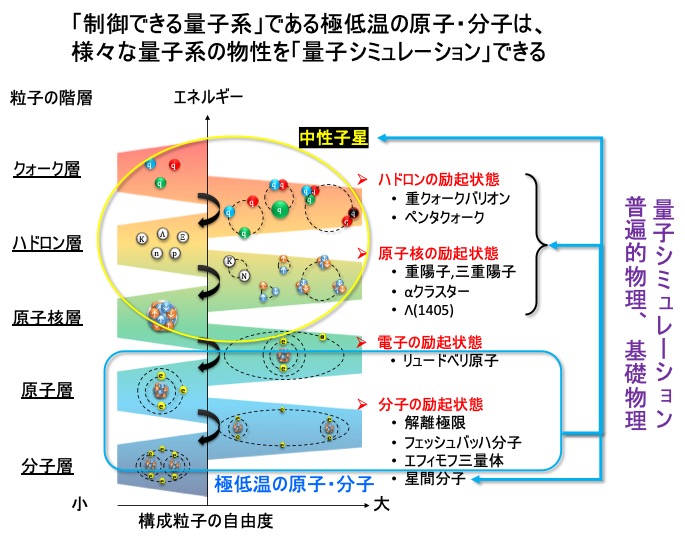
研究内容：豊富な内部自由度を持つ基本粒子がどのような量子クラスター状態を形成し、その基本粒子の自由度がクラスター形成に伴いどのように消失していくのか、またそのような振る舞いはどの観測量に現れるのかを理解することは、クォークから原子・分子へ至る物質階層科学の発展において必須である（下図）。特に異なる粒子階層間に存在する、相互作用距離よりも離れているけどギリギリ束縛するような「量子クラスター」状態は、「ユニタリ極限」と呼ばれる領域に近い。ユニタリ極限では粒子の詳細に依らない普遍的な量子物性が現れる領域であり、2004年に冷却原子実験で実現された比較的新しい量子系であります。本計画研究では「制御できる量子系」である極低温の原子・分子を用いて、様々な量子系の物性を「量子シミュレーション」することにより、「量子クラスター形成による複合粒子化」と「その量子クラスターが示す量子物性」の研究を進め、量子シミュレーションとして他の粒子階層への応用、普遍的物理の探査、基礎物理を深化させる。
具体的には以下の研究が進行中である。

  • ユニタリフェルミ気体の体積粘性率の測定（東大と東工大との共同研究）
  • フェッシュバッハ共鳴を用いた磁場中励起分子状態の精密分光（京大との共同研究）
  • BCS-BECクロスオーバーにおける状態方程式（慶大との共同研究）
  • スピンインバランス系におけるポーラロンの状態方程式、フェルミ粒子系負符号問題への挑戦（理研との共同研究）

Cluster

その他進行中の研究プロジェクトとこれから行いたい研究

  • 相互作用していないボース粒子の相転移の物理（東大との共同研究）
  • 同じエネルギーのフェルミ粒子とボース粒子を交換したらどうなるか？超対称性の検証
  • リチウム６原子とリチウム７原子間のフェッシュバッハ共鳴の探査、ボース・フェルミ混合系
  • 光デバイスを用いた冷却原子の動的操作
  • フェッシュバッハ共鳴の光制御による有効長の制御、冷却原子実験による核物質の基礎研究
  • ポテンシャル中を動き回っている原子１つ１つのイメージング、多粒子系の波動関数の観測
  • 非弾性散乱の可視化と、冷却原子加速器によるハドロン実験の量子シミュレーション
  • 1つ1つの原子から多原子分子への量子化学合成
  • 星間物質の応用へ向けた光化学反応
  • 少数系から多体系への化学反応論の変化
  • 京コンピュータや量子コンピュータの能力を遥かに越す量子シミュレータの開発、量子化学計算や少数・多体系への応用
  • 量子シミュレーションのクラウド利用化に向けたプラットフォーム開発
  • 機械学習を用いた実験装置メンテナンスの自動化

実験装置

我々はフェルミ粒子であるリチウム６原子とボース粒子であるリチウム７原子を用いて研究を行なっています。 どちらの原子もフェッシュバッハ共鳴と呼ばれる粒子間の相互作用の制御が可能であり、 どのような相互作用でどのような物性が現れるのか系統的に研究することができます。
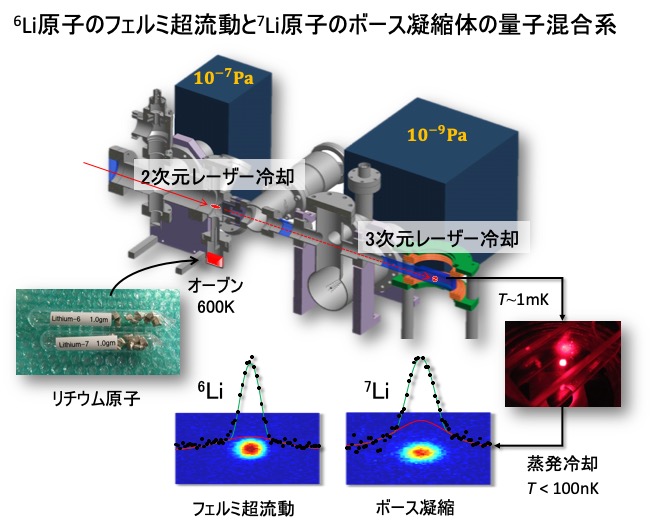
下図に実験装置の概略図を示します。 真空チャンバー中にリチウム原子のオーブンがあり、３４０℃（約600K）にリチウム原子を加熱し気化させます。 オーブン直上で２次元レーザー冷却を行い、冷えた原子のみを超高真空のチャンバーにレーザー光で送り、３次元レーザー冷却で捕獲します。 ３０秒のレーザー冷却で１mK程度の冷却原子を１０の８乗個程度集めることができます。 冷却原子はレーザー光の吸収・放出を繰り返すため、レーザー冷却の光の波長で光って見えます。 リチウム原子の場合λ=６７１nmであるため、赤く光る星のように目視で確認できます。 レーザー冷却で集められた冷却原子はさらに温度を冷やすために、光の容器に閉じ込められ、蒸発冷却という手法で1μK以下にまで冷却されます。 この時、原子の運動量は十分小さくなるため、不確定性原理より物質波の波長が大きくなり、物質波のド・ブロイ波長は１００nmにまで大きくなります。 粒子の平均粒子間距離も同程度であるため、この極低温の原子気体は粒子が相互作用する描像から、波同士が干渉し合う量子力学の描像に変化します。
さらに温度を冷やすことにより、フェルミ粒子はクーパー対を形成しフェルミ超流動状態を実現し、ボース粒子はボース・アインシュタイン凝縮（BEC）状態を実現します。我々は同じ光の容器の中で、リチウム６原子のフェルミ超流動とリチウム７原子のボース凝縮体が同時に実現されている量子混合系の実現に成功しています。この装置を用いて様々な量子系の物性研究を行なっています。
Apparatus

これまでの研究成果の紹介

引力相互作用しているボース粒子のBEC相転移の研究

ボース統計に従うボース粒子は化学ポテンシャルがゼロになる位相空間密度において、熱的状態に占有できる粒子数が飽和し、それ以上の位相空間密度の条件では粒子数を増やすためには基底状態に入るしか選択肢がなく、結果として基底状態にマクロな粒子数が占有しているボース凝縮状態(BEC)が実現されます。この現象は統計力学で学びますが、それではボース粒子はどのように位相を合わせて一粒子状態に入っていくのでしょうか？１つの量子状態にマクロな物質波が共存するためには、位相が合っていないと波動関数が打ち消し合うためマクロな波動関数を実現することができません。この位相を合わせるダイナミクスはKibble?Zurek mechanism (KZM)と呼ばれる理論モデルにより、粒子系に依らず普遍的に成り立つと信じられています。KZMを簡単に説明すると、位相を空間的に一様にそろえようとする速度と、どの範囲まで位相をそろえられるかの距離が相転移点からのズレの関数と臨界指数で与えられ、結果として相転移点を通過する速さによって位相がそろう領域が決まるというモデルです。よって、あまりにも速く相転移点を通過すると（本実験では相転移温度を通過する単位時間当たりの温度変化率）、下図のように位相欠陥があるBECが生成されます。
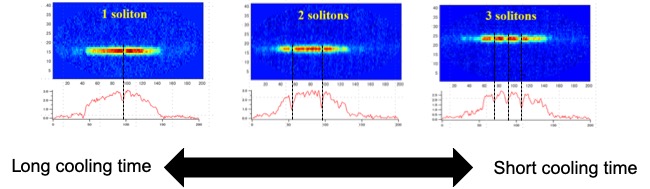
RepBEC

上の図は斥力相互作用しているボース粒子の場合の実験結果で、位相欠陥はダークソリトンとして観測されます。 ダークソリトンの数と相転移点を通過する速さの関係は、我々の実験結果も先行研究もKZMでよく説明できています。

それでは引力相互作用しているボース粒子ではどうであろうか？同じ物理法則に従うであろうか？KZMが相互作用の符号が異なる場合においても同様に成り立つことは、これまで実験的に確認されていませんでした。非自明な点として①引力相互作用しているBECは準安定状態であるため、BEC状態が安定な斥力相互作用と同じかどうか？②引力相互作用しているBECはどのように観測されるのか？③直感的には斥力より引力の方がBECになりやすく位相がそろいやすい気がするが、それでもKZMが動的相転移を支配しているのか？の３点がありました。

そこで我々は非常に弱く引力相互作用しているボース粒子を用いて検証実験を行ないました。一般的に引力相互作用しているBECはすぐに崩壊してしまいますが、我々はリチウム７原子のフェッシュバッハ共鳴を用いて散乱長を非常に小さい値(as~10a_0)に調整し、数千個の粒子数でも安定な引力BECを用いて実験を行いました。冷却速度に依存した生成された引力BECの典型例を下図に示します。
AtrBEC

斥力BECとは対照的に、相転移点を通過する速さに応じてブライトソリトンの数が変化しました。KZMと比較することにより、ブライトソリトンの数はKZMで予想される振る舞いと良く合っていました。 故にこの実験によって、相互作用の符号に依らず、また準安定状態のBECであっても、動的相転移の物理は普遍的にKZMで説明できることが実証されました。
それでは相互作用を全くしていないボース粒子の相転移の様子はどうだろうか？この問いの答えは誰も知りません。現在研究です！

[参考文献]

  • Yiping Chen, Munekazu Horikoshi, Kosuke Yoshioka, Makoto Kuwata-Gonokami, “Dynamical Critical Behavior of Attractive Bose-Einstein Condensate Phase Transition”, Phys. Rev. Lett. 122(4), 040406 (2019).

冷却原子実験による希薄中性子物質の物性研究

この研究は冷却フェルミ原子実験で中性子のみから成る希薄な中性子物質の状態方程式を決定した研究です。 本研究は、2012～2016の期間で活動していた新学術領域研究「実験と観測で解き明かす中性子星の核物質」の一環で進められました。 下図に中性子星の内部の密度分布を与える状態方程式の概念図を示しています。 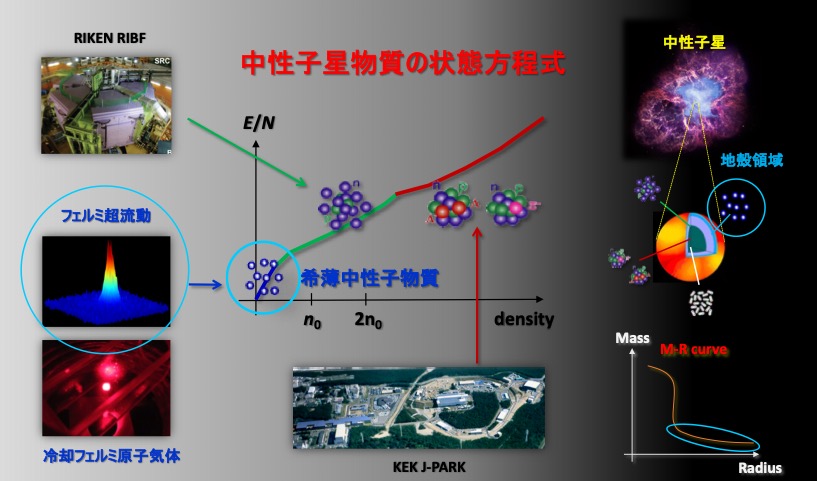NStar 本プロジェクトでは冷却原子実験と、日本を代表する理研のRIBFとKEKのJ-PARCの２大加速器実験で中性子星内部のそれぞれの密度領域の状態方程式を決定し、 X戦望遠鏡による観測により実際の中性子星の半径と質量の関係が決定された状態方程式によって正しく説明できるか評価するプロジェクトでした。 中性子星の中でも地殻領域から外核にかけての密度領域では、フェルミ粒子である中性子がクーパー対を形成し超流動状態を実現していると予想されています。 また中性子物質の状態方程式は中性子星の誕生の仕方、冷え方、地殻変動の様子と関係があります。 中性子星の地殻変動の様子は地球上でもパルサーの周期の変動の様子から捉えることができますし、 中性子星の温度の変化を観測し続けることにより中性子星が超流動転移を起こす様子も確認することができるそうです。 さらに中性子連星合体は重元素合成の工場と言われており、地球上の鉄以上の重元素は宇宙のどこかでぶつかった中性子星から生まれたものかもしれません。 中性子連星合体における元素合成は高密度核物質の物理が重要になりますが、複雑な物理も基礎から理解していく必要があり、その出発点となるのが低密度の中性子物質となります。 原子核の物性研究の観点で見ると、中性子物質の状態方程式は原子核の分極率や中性子過剰原子核の構造にも影響を与えます。 このように希薄な中性子物質の状態方程式の研究は、高密度核物質や中性子星の謎を解き明かす玄関口として非常に魅力的な研究課題であります。
中性子物質は中性子からなる物質なので研究領域は核物理学と思われがちですが、加速器等を用いた原子核実験にも得意不得意があります。 特に一様系の低密度核物質の研究は不得意な研究領域だと私は理解しています。そこで低密度核物質と同じ物理を示す極低温の原子気体が出番となるわけです！
もちろん原子で核物質の研究？と思われる方もいらっしゃると思いますが、実は原子や核子に限らず、ある条件を満たすと全て同じ普遍的な物理法則に従うようになります。 その条件は、近距離ポテンシャルで低エネルギー散乱している量子系であるということです。 この条件のもとでは、相互作用の影響は相互作用ポテンシャルの形状の詳細が散乱長(a)と有効長(re)という2つのパラメータに繰り込まれてしまいます。 つまり形状の異なる2つのポテンシャルでも両者が同じ散乱長と有効長を与えるならば同じ物理現象を示すことになります。 さらに散乱長と有効長というパラメータで相互作用している量子多体系の物性は、散乱長や有効長の絶対値が重要ではなく、 粒子系密度で決まる長さスケールとの無次元量が重要であることが熱力学関係式より証明できます。 故に冷却原子系はサブマイクロメートルの長さスケール、中性子物質はフェムトメートルの長さスケールと大きく異なっていても、 無次元化された物理系で比較すると全く同じ物理法則に従うことが理解できます。 最後に冷却原子系の伝家の宝刀であるフェッシュバッハ共鳴によって相互作用領域を中性子物質に調整してあげることにより、 実験室で中性子物質の量子シミュレーションが可能になるわけです。
EOS

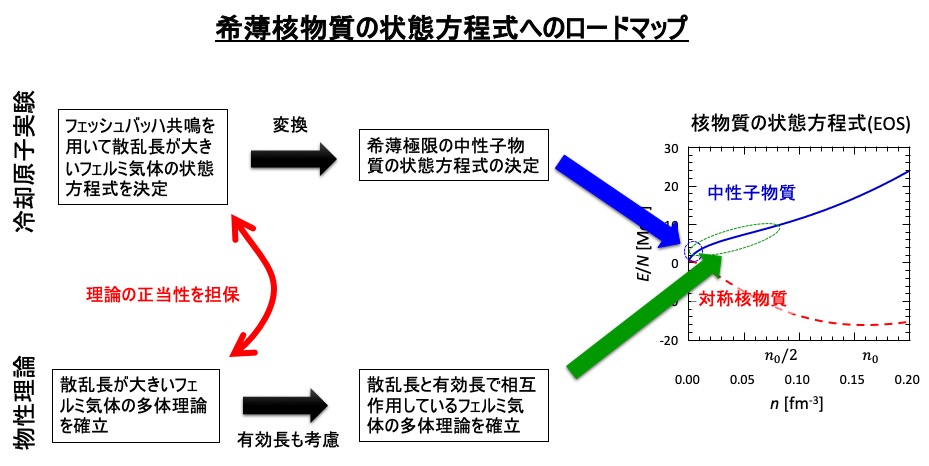
上図に我々が希薄中性子物質の状態方程式の決定に至ったロードマップを示します。 目的を達成させるため、物性理論と協力して研究を進めました。 冷却原子実験ではフェルミ粒子であるリチウム６原子を用い、フェッシュバッハ共鳴で散乱長を中性子物質の相互作用領域に調整し、フェルミ多体系の普遍的な状態方程式を決定しました。 得られた普遍的な状態方程式に中性子の質量や散乱長を考慮することにより、理論モデルに依存することなく希薄極限の中性子物質の状態方程式を示すことができました。 ただし現段階では冷却原子系で有効長の制御技術が確立されておらず、有効長が重要になってくる高密度領域の量子シミュレーションはできないのが現状です。 そこで我々の実験結果を説明できる物性理論を確立し、その理論に有効長の効果を取り入れることにより、飽和核密度の半分程度まで状態方程式を示すに至りました。 ご興味ある方は参考文献をご覧になって下さい。
本研究で大きな意義のある点は、冷却原子系で研究領域の異なる量子系の物性研究を実証した点であり、今後ますます冷却原子研究の活躍の場が広がることは間違いないと確信しています。 また有効長の制御技術が実現されれば、ハドロン系の量子シミュレーションの幅が広がるため是非手に入れたいです。現在研究中です！
[参考文献]

  • Munekazu Horikoshi and Makoto Kuwata-Gonokami, “Cold atom quantum simulator for dilute neutron matter”, International Journal of Modern Physics E Vol. 28, No. 1, 1930001 (2019).
  • Munekazu Horikoshi, Masato Koashi, Hiroyuki Tajima, Yoji Ohashi, and Makoto Kuwata-Gonokami, “Ground-state thermodynamic quantities of homogeneous spin-1/2 fermions from the BCS region to the unitarity limit”, Phys. Rev. X 7, 041004 (2017).
  • H. Tajima, P. van Wyk, R. Hanai, D. Kagamihara, D. Inotani, M. Horikoshi, Y. Ohashi, “Strong-coupling corrections to ground-state properties of a superfluid Fermi gas”, Phys. Rev. A 95, 043625 (2017).
  • H. Tajima, P. van Wyk, R. Hanai, D. Kagamihara, D. Inotani, M. Horikoshi, Y. Ohashi, “Zero-Temperature Properties of a Strongly Interacting Superfluid Fermi Gas in the BCS?BEC Crossover Region”, Journal of Low Temperature Physics, 1-8 (2016).
  • 堀越宗一, “s波散乱長で支配される普遍的物理法則”, 原子衝突学会学会誌「しょうとつ」, 2017年9月15日.
  • 堀越宗一, “冷却原子実験から希薄中性子物質へ”, 原子核研究 第61巻1号, 58-69 (2016).

吸収撮像法によるリチウム原子の精密測定に関する研究

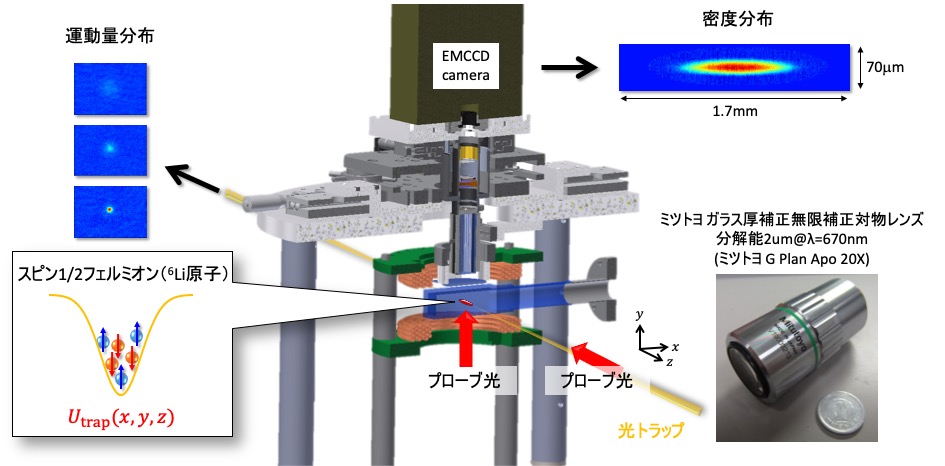
冷却原子実験で最も重要な技術の１つがトラップ中原子の精密測定技術です。 我々は冷却原子の観測手法として吸収撮像法を用いており、冷却原子に共鳴周波数のプローブレーザーを照射し、ランベルト・ベールの法則に従って透過してきた光をCCDカメラで撮影することで原子の密度分布を測定しています。ここで重要なのが、ランベルト・ベールの法則に従う条件でプローブ光を照射する必要がある点です。リチウム原子は軽い原子であるため、光子の運動量によるキック（光子反跳）の影響を大きく受けます。 このため共鳴周波数のプローブ光を照射していても、光子の吸収を繰り返すことにより原子が加速されていき、ドップラー効果によって共鳴周波数が変化してしまいます。さらに光子を放出する際はランダムな方向に光子を放出するため、その反作用でランダムウォークを繰り返し、この影響で撮影分解能が減少する問題が生じます。しかしこの２つの問題を回避するため短いパルス光を当てた場合、CCDカメラに届く光子数が少なくなりS/Nが悪くなるため、強度の強いパルス光を照射する必要が出てきます。その場合、光励起の飽和の影響を考慮する必要が出てくるため、実験系を考慮した実効的な飽和パラメータを評価する必要が出てきます。 このようにリチウム原子を高精度に観測するためには注意しなければならない項目があるのですが、本研究で我々は最適なプローブパルス光の条件を実験と理論で説明し、実効的な飽和パラメータを容易に決定できる手法を開発しました。また、２μmもの高い光学分解能を有しているため詳細に冷却原子の情報を得ることができます。
本研究成果により、我々は自信を持って定量評価が行えるようになりました。撮像セットアップの概略図は以下のような感じです。ご興味ある方は参考文献をご覧になって下さい。
image

参考文献

  • Munekazu Horikoshi, Aki Ito, Takuya Ikemachi, Yukihito Aratake, Makoto Kuwata-Gonokami, and Masato Koashi, “Appropriate Probe Condition for Absorption Imaging of Ultracold 6Li Atoms”, J. Phys. Soc. Jpn. 86, 104301 (2017).



フェルミ超流動とボース凝縮体の量子混合系に成功した研究

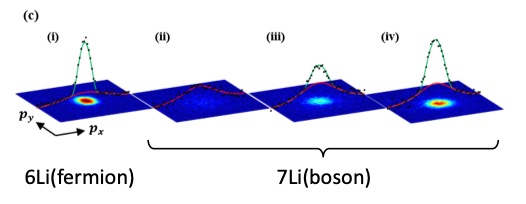
我々は強く相互作用しているフェルミ粒子系の量子物性に興味を持っており、その温度評価を行うために温度計として他の原子を希薄に混ぜる手法を考えていました。 ここでフェルミ粒子はリチウム６原子で、ボース粒子はリチウム７原子です。 我々はまずリチウム６原子単体でフェルミ超流動状態を実現しました。下図はフェルミ対の重心運動量分布を測定したものであり、 熱的成分と凝縮成分の２成分がバイモーダル分布している様子がわかります。 そこにリチウム７原子も混合させることにより、リチウム６原子との熱接触によりどんどんボース粒子の温度が下がり、以下の図のように最終的にボース凝縮状態に至りました！ これによってフェルミ超流動とボース凝縮体の量子混合系が実現されました。 後に我々はボース粒子の冷却速度がフェルミ粒子の温度を制御することによって可能になることに気づき、上で紹介しているボース粒子の相転移のダイナミクスの研究に発展しました。 今後、リチウム６原子とリチウム７原子間のフェッシュバッハ共鳴が見つかり制御できる湯になると、さらに研究の幅が広がるでしょう。現在研究中です！
Mix 参考文献

  • T. Ikemachi, T. Ito, Y. Aratake, Y. Chen, M. Koashi, M. Kuwata-Gonokami, and M. Horikoshi, “All-optical production of dual Bose-Einstein condensates of paired fermions and bosons with 6Li and 7Li”, Journal of Physics B: Atomic, Molecular and Optical Physics, 50(1), 01LT01 (2017).

ユニタリフェルミ気体の熱力学関数を世界で初めて測定した研究

近距離ポテンシャルに対して低エネルギー散乱している粒子系の相互作用は、散乱長というパラメータで記述できます。散乱長は任意の値をとることが許されており、物理的な意味は近距離ポテンシャルへアプローチする波動関数の形で定義されます（ベーテ-パイエルス境界条件）。散乱波の位相シフトや波の仮想的な反射位置としても解釈可能です。（ただし散乱長が無限に発散している場合、反射位置として考えるとよくわからなくなります）散乱長が±?に発散している状況をユニタリ極限と呼び、物理的状況として散乱ポテンシャルの束縛状態が入射エネルギーと等しくなる場合に相当します。粒子がフェルミ粒子の場合ユニタリフェルミ気体、ボース粒子の場合ユニタリボース気体と呼びます。勘違いされやすいのが、二粒子間の散乱長が発散している場合、宇宙の端と端の粒子が相互作用できると誤解される方がおられますが、粒子は相互作用ポテンシャルの相互作用領域まで近づいて初めて相互作用し、その散乱振幅が散乱長の関数で記述できるだけです。また、散乱長が無限だからといって相互作用の強度が無限に大きくなることもなく、量子力学で粒子間の相互作用の大きさは制限されています。

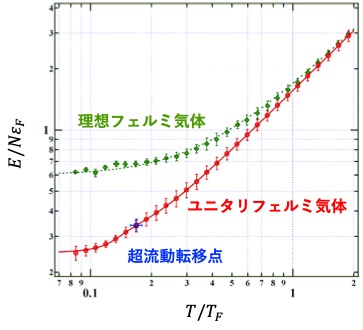
ユニタリ極限は様々な量子系で起こり得る状況ですが、散乱長が無限に発散すると散乱長は量子系を記述するよいパラメータではなくなってしまうため、相互作用しているにも関わらず相互作用を与えるパラメータが消失してしまいます。このような量子系では平均粒子間距離（またはフェルミ波数）と熱的ド・ブロイ長の2つの長さスケールにか存在せず、故にユニタリ極限に属する全ての量子系の物性は、T/TFという無次元温度のみに依存する普遍的な物理法則位従うことが期待されます。しかし理論的にユニタリ極限を扱うのは困難であり、容易にユニタリフェルミ気体を実現できる冷却フェルミ原子系の出番となります！

我々がユニタリフェルミ気体を研究し始めた当時は調和ポテンシャル中の研究が大半であり、局所密度で決まる一様系の状態方程式は決定されていませんでした。我々は先行研究をヒントに、調和ポテンシャルの測定データから一様系の物理情報を導出する手順を見出し、世界に先駆けてユニタリフェルミ気体の普遍的な熱力学関数を以下の図のように示しました。本研究を皮切りにユニタリフェルミ気体の状態方程式の測定精度が向上し、それに伴い理論研究も大きく進展致しました。ご興味ある方は参考文献をご覧になって下さい。
Unitary 参考文献

  • Munekazu Horikoshi, Shuta Nakajima, Masahito Ueda, Takashi Mukaiyama, “Measurement of Universal Thermodynamic Functions for a Unitary Fermi Gas”, Science 22 Vol. 327 pp. 442-445 (2010)
  • 堀越宗一, 向山敬, 上田正仁, “ユニタリー極限におけるフェルミ原子気体の普遍的熱力学”, 日本物理学会誌 Vol. 67, 2012年4月号, p. 257-261.

これまで獲得した競争的資金

  • 新学術領域研究(研究領域提案型)：実験と観測で解き明かす中性子星の核物質
    計画研究：冷却原子を用いた中性子過剰な低密度核物質の状態方程式
    研究期間 (年度)：2012～2016
    研究代表者：堀越 宗一, 東京大学, 大学院理学系研究科(理学部)
    研究分担者：中務 孝, 筑波大学, 数理物質科学研究科(系)
    向山 敬, 電気通信大学, レーザー新世代研究センター
  • 若手研究(A)：強相関フェルミ原子気体の二流体現象の観測と輸送係数の測定
    研究期間 (年度)：2011～2013
    研究代表者：堀越 宗一, 東京大学, 工学(系)研究科(研究院)

受賞等

  • 堀越宗一、日本物理学会若手奨励賞「冷却フェルミ気体における普遍的熱力学関数の決定」、2012年9月